“There are three kinds of lies: lies, damned lies, and statistics.”
Correlation is not causation is the mantra of introductory statistics classes, but professors sometimes grow weary of saying it in the same way and seeing the warning ignored by even professional researchers. This is what led Robert Matthews, then of Aston University, to conduct a statistical analysis of the relationship between birth rates and stork populations.
In an article for Teaching Statistics, Matthews explains that the usual examples for illustrating that correlation is not causation — such as the relationship between children’s shoe size and reading level — suffer from being too obvious. (In the reading ability example, shoe size reflects the confounding variable of the children’s age, which is what best explains their reading ability.) What is needed, Matthews writes, is an “example based on genuine data of an association which is clearly ludicrous, but which cannot be so easily dismissed as non-causal” due to an obvious confounding variable like in the reading ability example.
Enter the storks delivering babies story.
While associations between storks and fertility appear in as old and diverse mythologies as Greek myths and Ancient Chinese stories, the modern story seems to come from 18th and 19th century Germany. Storks are migratory birds that would return to Germany in spring, about 9 months after midsummer and prime babymaking times, which led to stories about people leaving candy out for storks when they want a baby. Today the continued popularity of the story gives parents of young children an easy out when asked where babies come from.
Children learn the truth in good time, but Matthews rhetorically asks how a scientist would refute the story. He writes:
If one were approaching the question in the same way that many other links are investigated (e.g. suspected links between diet and cancer risk), one may well decide to carry out a correlational study, to see if the number of storks in a country bears a simple relationship to the number of human births in that country.
So Matthews looked up the data and did just that, leading to the following chart:
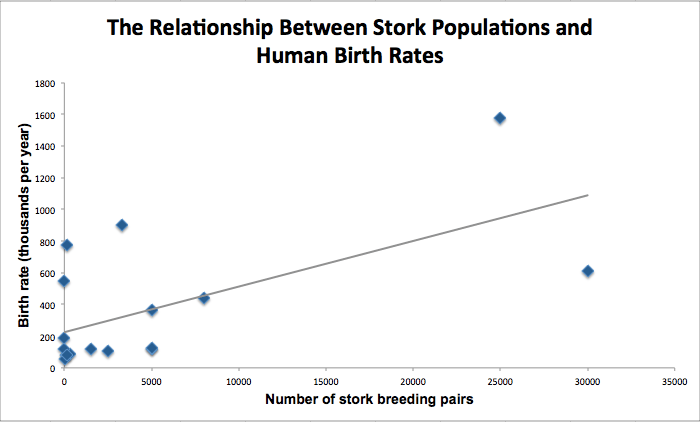
Adapted from Matthews, “Storks Deliver Babies (p = 0.008).” Data from 1990.
Lo and behold, a correlation exists between the number of births and the number of storks in a country.
The relationship is not extremely strong. Between a perfect correlation of 1 and a correlation of zero that would indicate no relationship, the correlation between the stork population and birth rate is 0.62. But as Matthews points out, using a standard technique to assess the significance of the correlation reveals that there would be “only a 1 in 125 chance of obtaining at least as impressive a value” if there were no relationship between stork populations and human birth rates. (Or in technical terms, p = 0.008.)
Storks don’t deliver babies, but as Matthews writes, interpretations of statistics in this case would far too often say that there is only a 1 in 125 chance that storks don’t deliver babies. Instead researchers should consider what else may explain the correlation — a confounding variable like age in the shoe size and reading level example.
A few factors impact how many storks inhabit various European countries, such as pollution, conservation efforts, and the habitat. But a simple variable that affects both the birth rate (which is not per capita) and the stork population is the size of each country. Following Matthews’s instructions, we show below how land area contributes to the correlation (but not causation!) between the number of storks and delivered babies.

This post was written by Alex Mayyasi. Follow him on Twitter here or Google Plus. To get occasional notifications when we write blog posts, sign up for our email list.




