
Imagine that you are honored for your work with the equivalent of a Nobel Prize in your field — an elite award for your marketing career perhaps, or a most valuable player distinction if you are a professional athlete. What do you do next?
Do you redouble your efforts to distinguish yourself and live up to your elite status? Do you switch to more of a consulting and mentorship role? Or do you relax and enjoy some well-earned rest? This is the driving question of a working paper from George J. Borjas of Harvard and Kirk B. Doran of Notre Dame entitled “Prizes and Productivity: How Winning the Fields Medal Affects Scientific Output.”
The two focus on the Fields Medal, which is often referred to as “the Nobel Prize for mathematics,” as it is only awarded to relatively young mathematicians. (Only those under 40, as of 2006.) As the authors note, the prize money and prestige of awards is often used to incentivize achievement. By looking at a medal awarded mid-career, Doran and Borjas investigate whether such honors still inspire achievement once they have been awarded — a stated goal of the Fields Medal.
To determine whether the productivity of mathematicians increased or decreased after winning the Fields Medal, the authors take advantage of the fact that not every deserving mathematician wins a Fields Medal. (The number of medals awarded is set by the funding available — not the number of significant contributions made by young mathematicians every year.) So, Doran and Borjas assembled a group of “contenders” that led equally productive careers based on two criteria: winning one of 6 other nearly-as-prestigious mathematical awards and the number of papers that cited their publications.
As we see in the below comparison of Fields winners and Fields contenders, winning the Fields Medal seems to be a major drag on productivity:
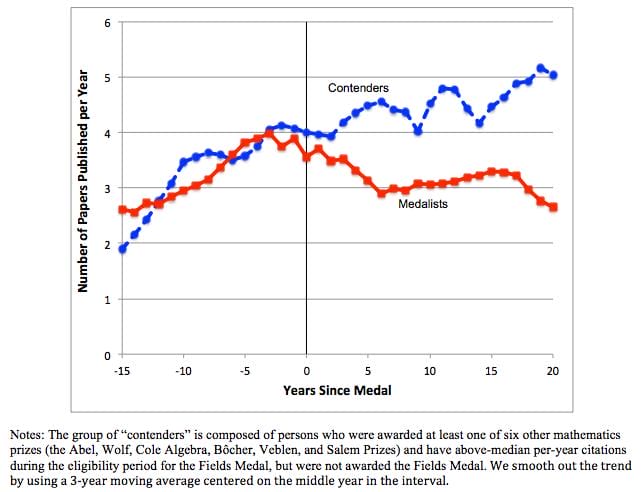
The above graph shows a drop in the number of papers medal-winners publish. The same decline is also seen in the number of times the winners’ papers are cited by other mathematicians — a common metric of a paper’s quality or “impact” — both in total and per paper.
The authors also rule out the possibility that the winners publish less in order to focus on teaching and mentoring. In fact, the winners’ teaching seems to suffer the same productivity dip: The medal-winners take on fewer graduate students compared to the comparable “contenders,” and those graduate students also publish fewer and less impactful papers.
So what happens? Do the winners get complacent while their non-medal winning peers remain driven?
Not exactly. As the authors write:
“The medalists begin to ‘play the field,’ studying unfamiliar topics at the expense of writing papers.”
Doran and Borjas refer to this research into topics outside the mathematicians’ core area of study as “cognitive mobility.” Secure in their positions thanks to the Fields medal, the winners feel free to take more risks and study topics outside their core competency — at the cost of churning out papers.
By mapping the relatedness of different subject categories, the authors come up with the following chart showing how medal-winners write papers in very areas of mathematics outside their own specialty or even outside mathematics altogether:

By looking at the increased amount of time medal winners spent writing papers outside their core area of expertise, Doran and Borjas do a “back-of-the-envelope” calculation (using a regression) and find that about 50% of the decline in the medal-winners’ productivity can be traced to cognitive mobility. The remaining 50% they ascribe to the “wealth effect” of mathematicians choosing to work less after winning the Fields Medal. (The $15,000 prize money is not huge, but the prestige offers job security and career opportunities.)
So should organizations stop giving out awards lest they inspire sloth in the winners?
The authors caution that the Fields Medal may be a particular case. It is awarded mid-career rather than at the finale of one — as is more common with a prize like the Nobel. Mathematics is also distinct in that it usually does not require expensive infrastructure such as lab equipment and huge teams of researchers. In a field that does, winning a prestigious prize could improve productivity by making it easier for the scholar to bring in funding.
It’s also unclear whether this decline in the productivity of the Fields Medal winners is a negative development. While number of papers published and number of citations are widely used measures of productivity, any number of academics will complain that they do a poor job of capturing the real worth of research. Which is better: publishing dozens of incremental papers in one area or publishing one paper that redefines a number of fields?
Doran and Borjas make this point, noting that the medal-winners’ “playing the field” could allow them to make contributions in “previously underserved” areas of research. In fact, they point out that there are 3 prominent examples of Fields Medal winners that went on to do breakthrough work outside pure mathematics.
The authors quote a passage about one such mathematician, Stephen Smale, to show how the prestige of winning the Fields Medal may have been beneficial in allowing him to take the risk of pursuing research outside his own field:
Smale [was]. . . already famous for unraveling the most esoteric problems of many-dimensional topology. A young physicist, making small talk, asked what Smale was working on. The answer stunned him: “Oscillators.” It was absurd. Oscillators—pendulums, springs, or electrical circuits—were the sort of problem that a physicist finished off early in his training. They were easy. Why would a great mathematician be studying elementary physics?
It would be a much more ambitious project to say whether the contributions of Fields winners outside their core area of mathematics are worth the loss of productivity. It’s a small sample to look at by the data, and comparing the value of papers in different fields and of incremental versus more fundamental papers at some point becomes a normative question.
But depending on whether you see advances in research and new discoveries taking place incrementally or in punctuated equilibrium, the average effect of the Fields Medal — to make mathematicians more “lazy,” curious, daring, and inured to the “publish or perish” culture of academia — is exactly the type of support an award like the Fields Medal should provide.
This post was written by Alex Mayyasi. Follow him on Twitter here or Google Plus. To get occasional notifications when we write blog posts, sign up for our email list.



