What’s the best way to cut a cake?
Unless you’re a professional wedding planner, you probably haven’t given the question much thought.
You might think the answer is simple. Just count the number of diners at the table and divide up the frosting-coated surface evenly. Diets and gluten allergies might complicate your calculations, but really, you might think, this isn’t advanced mathematics.
Except advanced mathematics is exactly what this is. And clearly you have failed to ask the important questions.
For example, does your cake-cutting procedure guarantee that no one will leave the party feeling that they got a lesser piece than anyone else?
Have you taken steps to ensure that each cake-eater is deriving equal joy from his or her allocated slice?
Did you even think to split up the cake in such a way that no guest could be given a better slice without degrading the quality of someone else’s?
Maybe by now you’ve figured out we aren’t just talking about cake.
Within the field of “fair division” problem solving—which sits at the crossroads of mathematics, political science, and economics—cake is more than just a dessert. Cake is an apartment building with rooms to be assigned to picky housemates. Cake is a high stakes divorce settlement. Cake is a war-torn country. Since the 17th century, theorists have been devising methods to divvy up the things we all want in ways that obey both the rigid formalism of mathematics and our more subjective notions of fairness. All the while, cake has been used as a powerful metaphor for all that is good, finite, and divisible in the world.
And now, with recent advances in fair division theory and computer science, a growing number of researchers want to make these methods available to the inexpert and conflict-prone public. With the click of a button, you too can cut a cake like a mathematician.
Choosy Moms Choose Fair Division
Children have long known the best way to divide a coveted object in two. The method is called “I cut, you choose,” or some variant thereof, and you probably ran this fair division algorithm with your friends when you were in elementary school.
If not, allow the “choosy mom” of mid-2000s Jif peanut butter ad-dom to explain:
Jif Peanut Butter, touting the wisdom of fair division algorithms since 2006.
The Solomonic, Jif-eating brothers are in good company. English children were doing virtually the same thing as early as the 17th century. As the political theorist James Harrington noted in 1656, “that which great philosophers are disputing upon in vain is brought to light by two harmless girls.”
“For example, two of them have a cake yet undivided,” he wrote. “Each of them therefore might have that which is due, ‘Divide,’ says one to the other, ‘and I will choose; or let me divide, and you shall choose.'”
The genius behind the method is not only that it’s simple enough to implement on a playground, but also that it produces results which are, at least in certain circumstances, intuitively fair. The cutter knows that the chooser is going to pick the better of the two halves, so she cuts the cake as evenly as possible. Both sides are guaranteed a slice of the cake that they believe is at least as good as the other.
Economists and mathematicians have since given this quality the uninventive label “envy-free.”
Envy-freeness is exactly what it sounds like. If you have a vanilla cake and you need to split it between two people, both of whom like vanilla cake equally, then the envy-free distribution is pretty easy to figure out. Just cut the cake in half. Both sides feel that they got at least as much as their counterpart, because they got exactly as much. No advanced degree in mathematics required. Envy-free is a piece of…well, you know.
The “I cut, you choose” method can work not just for “goods” (cakes and peanut butter), but “bads” as well. As the popular mathematics writer Martin Gardner illustrated in comic form in 1978, chores can also be fairly divided as long as one person divides each task into two lists and the other chooses one as their own.
And, as it turns out, what’s good for children and comic books is often good enough for corporate lawyers too.
In the forging of joint ownership contracts, lawyers frequently include so-called “Texas shootout” provisions, which can be thought of as a monetary analog of “I cut, you choose.” In the sad event that one corporate party wishes to part ways with the other, one partner will name a price and the other chooses to either buy or be bought out at that price.
As James F. Ring writes, “the initiating party puts her adversary in a position where the adversary’s most sensible strategy is to make an honest appraisal and bring the dispute to an end.”
Ring knows from experience. As the co-founder of Fair Outcomes, Inc., a firm dedicated to helping estranged corporate partners and divorcees reach envy-free solutions with the help of proprietary fair division algorithms, he and co-founder, Steven Brams, have found plenty of uses for “I divide, you choose”—or more computationally intensive versions of it.
In an overview of fair division applications published in Nautilus, science writer Erica Klarreich offers one such example. In the event of the contentious breakup of a marriage or relationship, the algorithm, which Ring and Brams call “Fair Buy-Sell” requires each partner to simultaneously propose a price.
“If John proposes $110,000 and Jane proposes $100,000 then John, the higher bidder, will buy out Jane for $105,000,” explains Klarreich. “Each participant ends up with something—either money or the business—at a price that is better than his or her offer.”
“I cut, you choose” has even made its way into international maritime law. In the 1970s, as countries began contemplating a possible future in which undersea mining would become a major industry, developing countries grew concerned that technologically sophisticated corporations would purchase rights to the most valuable seabed before developing countries had a chance to establish their own surveying methods. A solution was proposed and ratified in the Convention of the Law of the Sea.
Now, if a company wishes to mine a tract of seabed, they must first propose a division of that tract into two parts. The home country then gets to choose one for itself.
Envy-Freeness and its Discontents
But as any elementary school student can tell you, there are some conflicts that even “I cut, you choose” isn’t equipped to handle.
Returning to the culinary metaphor, imagine if the cake in question isn’t plain vanilla (let’s say a few strawberry slices have been placed along the left edge) and that the hungry guests at the table have different preferences (maybe one person prefers fruit, while the other only has eyes for baked goods).
If the strawberry fan gets to cut, he might divide the cake in half horizontally, leaving an equal number of strawberries on either slice. This would leave him indifferent between the two slices and, more importantly, it would ensure that he gets his share of fruit, no matter how the cake-lover chooses.
Since the cake-lover is just going to throw her strawberries away, she too is indifferent between the two slices and would probably choose at random.
These results are once again envy-free. Neither party would want to switch slices with the other.
But there is still something unsatisfying about the outcome. Specifically, economists would call this result “inefficient,” because the slices could be rearranged in such a way to make at least one of the cake eaters better off, without making anyone worse off. In this case, there is an obvious improvement: the strawberry fan could swap some of his extra cake for her unwanted fruit. Everyone wins.
Is the lesson here that the strawberry fan simply made the wrong cut? Would it have been more efficient had he focused on the berries instead?
In fact, we can imagine another example (this one pinched with some modifications from a paper by Claus-Jochen Haake and Francis Su), in which the strawberry fan instead just cuts off the smaller berry-covered edge. This way, he is guaranteed either the smaller piece with the berries (which would be fine, because he likes fruit) or the big piece without the berries (which would also be fine because, his lack of berries notwithstanding, he still ends up with a lot of cake).
This time the choice for his counterpart is obvious. She would choose the bigger piece.
Now the results are efficient, because there are no obvious win-win trades to be made—the cake slices couldn’t be rearranged without making at least one of the parties worse off. Better yet, the results are also envy-free. Neither party has any reason to want to switch slices with the other. In theory, there is no cause for envy.
And yet, fickle human psychology has a way of muddying up mathematical models of human behavior. The solution above may be mathematically “envy-free,” but it doesn’t square with our basic sense of fairness. The strawberry fan is just breaking even (he gets a slice that he considers to be 50% of the cake’s value), while the cake lover, who is receiving the vast majority of the cake, is making out like a bandit.
Cake for Three, Cake for Four, and Cake for n
The trade-offs between envy-freeness, equitability, and efficiency is one that has beguiled theorists for decades. As one might expect, inviting additional cake eaters to the table introduces even more complexity.
In the 1940s, a Polish professor named Hugo Steinhaus was the first to tackle these questions with mathematical rigor. Asking whether there was a version of “I cut, you choose” for three or more people, he ultimately came up with what is now called “the lone divider method.”
Absent any Greek symbols, this algorithm can be illustrated by example. Imagine three would-be consumers of cake. One is chosen at random to be the “lone divider” and is asked to slice the cake into three pieces. As with “I cut, you choose,” the cutter doesn’t know which slice he is destined to get, and so he tries to cut three equally desirable slices.
The remaining two cake eaters, the choosers, are then asked to jot down which of the slices they would accept, if any. The lists are then compared. If the two choosers have declared themselves willing to accept different slices, then the game is over: the two slices are passed out accordingly and the lone divider gets the third.
If, however, the two choosers both want the same slice, then the lone divider is given one of the non-contested portions, and the two remaining slices are mushed back together. Now we have a single, smaller cake, two hungry competitors, and a game of “I cut, you choose” to play.
Steinhaus’ lone divider method is appealingly simple and can be extended to more than three players, but it fails to guarantee results that are either efficient or envy-free. For that, more complex math is required.
A Cake Composed of Triangles
Francis Su was getting his doctorate in math at Harvard in the late 1990s when Brad Mann, his friend and fellow PhD candidate, came to him with an all too common problem.
Like most students in the Cambridge area, Mann shared a cramped house with a few budget-conscious housemates. Naturally, opinions diverged over who was entitled to which room and for how much. Mann came to Su wondering how to break the impasse.
While most of us would have responded with a simple rule of thumb (“draw straws and split the rent evenly” or “nose goes for the room upstairs with the big closet”), Su, who is now a professor at Harvey Mudd College and President of the Mathematical Association of America, is not like most of us.
“When he told me his predicament, I said, ‘that’s a math question!’” he says. Specifically, it was a fair division question.
That revelation may not have been of much use to Mann, but a few years later, Su published a paper on the topic in which he was able to prove that in a house thus divided, rooms can be assigned and rent divided in such a way as to leave everyone “approximately envy-free,” thus achieving “rental harmony.”
As an application of the “age-old cake-cutting problem,” what made Su’s paper particularly innovative was his use of an obscure mathematical argument from the 1920s called Sperner’s Lemma.
The concept, in its most basic version, has nothing to do with rent or cake. Instead, it relates to triangles.
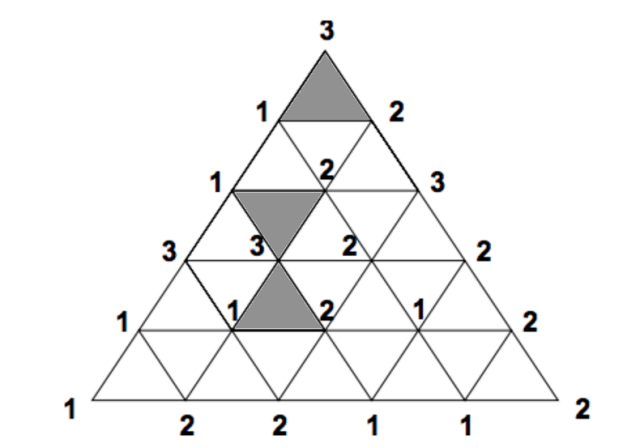
Image Source: Francis Edward Su
The setup goes like this:
Let’s imagine you have a large triangle, like the one above. Each of the points that lay at the end of the shape’s three large edges is given a number (in this case, 1, 2, and 3).
The triangle is then sliced up into a series of smaller triangles and the points at the end of each slice (called vertices) are also assigned one of those three numbers.
But there’s a hitch. Any vertex along the edge of the larger triangle has to share its number with one of the two points at the end of that edge. For example, the numbers along the bottom of the triangle are only allowed to be 1 and 2 because they sit between the two points of the larger triangle that are labeled 1 and 2. Likewise, the triangle’s left side can only have labels 1 and 3, while the right side only gets 2 and 3.
According to the “lemma” (a mini-theorem), if all of the above conditions are true, then there must be at least one triangle in the whole mesh of criss-crossing vertices that has a different number at each of its three points. In picture above, there are three.
What does any of this have to do with rent? This was Su’s insight.
In the paper, the triangle is reimagined as every possible combination of room prices, split up amongst the three rooms. The point at the top of the triangle, for example, might represent a situation in which one of the roommates is paying the entire rent bill on a Room A and the others are paying nothing for the remaining two rooms, Room B and C. Likewise, the point on the left corner of the large triangle would represent a situation in which Room B is saddled with the entire rent bill. Moving into the center of the triangle corresponds with more equitable divisions of rent amongst the three rooms.
As a procedure, Su imagined assigning “ownership” of each vertex, or price combination, to one of the housemates.
The algorithm would begin with a vertex at the outside of the triangle and ask its owner the following question: “If the rent were to be divided according to this pricing scheme, which room would you choose?” Depending on that housemate’s response, that point would be given a number (1, 2, or 3, corresponding to the room of choice). Then the algorithm could “move” to a new price-and-room combination deeper inside the triangle where the same question would be posed to the housemate that owns it.
This method would continue until a room pricing scheme was found where each housemate would agree to occupy a different room at that price point. Graphically, this point would exist within a triangle in which each roommate had labeled a different room at each point. Remember that according to Sperner’s Lemma, such a triangle has to exist. Q.E.D., rental harmony is possible.
Mathematical details aside, the paper was a hit. In 2014, the New York Times even made a rental harmony calculator using Su’s algorithm.
Fairness: There’s an App for That
Francis Su’s algorithm may have received the Times treatment, but it’s not the only online application that promises to offer fair solutions to envy-inducing problems.
That same year, a group of computer scientists at Carnegie Mellon launched Spliddit. While Su’s algorithm is iterative, requiring repeated inputs from each participant, and only offers envy-free solutions, Spliddit’s rent calculator aims to be both user friendly and a purveyor of solutions that are “provably fair.”
Finding the algorithmic special sauce for emotionally satisfying fairness required a little trial and error. While the first version of the application mimicked a room assignment algorithm developed in 2004, the results it produced, though envy-free in a strictly mathematical sense, were not always perceived as such by the humans who engaged with it.
“Sometimes you have solutions that satisfying some theoretical fairness guarantee, but some examples don’t do what you intuitively think is fair,” says Ariel Procaccia, the Carnegie Mellon professor who led the project.
He offers an extreme example. Imagine a three-room apartment split between three roommates. The rent is $3. Clearly, this is not in a coastal city.
The first housemate is only interested in living in the first room, the second housemates is only interested in the second, and third only has eyes for the third. Each housemate would be willing to pay the entire $3 rent for the room of his or her preference.
One possible split would be to put each housemate in the room of their choosing and assign the entirety of the rent to the first housemate. The second and third housemates are getting a much better deal, but even the first housemate has no reason to object. He is paying $3, exactly as much as he is willing to for his preferred room, and he has no interest in living elsewhere in the house.
Recalling the cake example, this is analogous to the strawberry fan getting the fruit-covered edge of the cake: he is breaking even while his competitor is getting a great deal.
“This is an envy-free solution, but it’s obviously not fair,” says Procaccia. “The intuitively fair thing to do would be to give everyone the room that they want and have each player pay $1.”
That is roughly what the Spliddit algorithm strives to do. First, it tries to maximize the difference between what a given housemate is willing to pay for a room and what he or she ultimately pays. This “surplus” measures just how good a deal each housemate is getting and the algorithm ensures that each housemate’s surplus is higher than the surplus he or she would receive in a different room. This satisfies the envy-free condition.
But then, in an attempt to find an “intuitively fair” solution, the calculator finds a combination of room assignments that minimizes the difference in the surpluses of each housemate.
In short, the algorithm guarantees that everyone gets a good deal, but that no one gets too good a deal compared to their fellow housemates.
Since its release, Spliddit has also branched out into taxi fare calculations, work credit allocators, task dividers, and an algorithm that divvies up sundry goods. In the meantime, Procaccia and a separate group of researchers are working on RoboVote, an application that aggregates the ranked preferences of different individuals in order to help them make smart collective decisions. He says the website is scheduled to launch at the end of this coming September. Schedule your arguments over where to go to dinner accordingly.
Still, Procaccia has set his sights a bit higher than that. One of the motivations behind producing Spliddit was to introduce the public at large to the benefits of computationally-assisted fair division problem solving methods. Just as “I cut, you choose” algorithms have been used to settle business conflicts, he hopes that one day computers will be called upon to help resolve much more complicated negotiations.
For Procaccia, who was born and raised in Israel, a particularly thorny one comes to mind.
“If something like [the Arab-Palestinian conflict] could be mediated by computers, that would be truly wonderful,” he says. “I think we are a far way from that utopia, but I think that’s definitely the end game.”
But first, theater seating.
Recently, Procaccia says he went to see a musical with a number of former grad school classmates and his Ph.D. advisor. One member of the group had purchased the tickets in bulk, but the seats were scattered around the auditorium and had fetched different prices. The computational social choice theorists put their heads together to decide how they might optimally cut this proverbial cake.
“We were talking about how you could use the rent division application of Spliddit, thinking about these seats as rooms and deciding who gets which seat and for what price,” he says.
But the group quickly ran into a problem. The value of a given room in an apartment doesn’t come with a pre-assigned price. The seats, in contrast, had their (in some cases, quite high) values printed right on the ticket stub.
“If the seat was bought for $200, and the algorithm tells you that you need to pay $220 for it, that has a negative psychological effect,” he says.
In the end, everyone just took the seat of their preference and agreed to pay the face value. As it turned out, it was just easier that way.
Our next article investigates the data behind interracial marriages in the United States. To get notified when we post it → join our email list.
![]()
Note: Check out Priceonomics Content Marketing. We have some free software you can use to measure content marketing performance.





