The legendary mathematician Carl Friedrich Gauss considered his alleged discovery of statistical regression “trivial.”
The method seemed so obvious to Gauss that he figured he must not have been the first to use it. He was sure enough it must have been discovered that he did not publicly state his finding until many years later, after his contemporary Adrien-Marie Legendre had published on the method. When Gauss suggested he had used it before Legendre it set off “one of the most famous priority disputes in the history of science…” Gauss would eventually be given most of the credit as the founder of regression, but not without a fight.
Gauss’s “trivial” invention is now at the center of modern statistics and data science.
Regression is a statistical tool for investigating the relationship between variables. It is frequently used to predict the future and understand which factors cause an outcome — if you want to figure out how schooling impacts wages, guess the winner of the next election, or figure out the impact of a new drug, there is a good chance you’re going to use regression. The historian of statistics Stephen M. Stigler calls regression the “automobile” of statistical analysis.
“… despite its limitations, occasional accidents, and incidental pollution, it and its numerous variations, extensions, and related conveyances carry the bulk of statistical analyses, and are known and valued by nearly all.”
So how did regression, so simple to Gauss, and so essential to much of modern science, arise? Does Gauss really deserve credit for the method’s discovery?
***
At the turn of the 18th Century, improving ocean navigation was perhaps the most important practical scientific problem of the day. The Age of Discovery had led to great riches and lucrative trade, but sea travel was still dangerous, and prone to inaccuracies. Improved technology in this area was worth a lot of money. With greater navigation precision, ships — and their cargo — would be more likely to reach their intended location safely and quickly.
Given the massive economic rewards of better navigation, geodesy, the study of the measurement of earth, was all the rage. At that time, a key tool of geodesists was the use of the movements of other planets and comets, relative to Earth, as a way to understand Earth’s shape and behaviors. This led to better mapping and improved knowledge of location, which in turn made it easier to find your way quickly and safely from Portugal to India. Monarchs and noblemen were happy to support research in this area.
It was in this historical context that the mathematicians Carl Friedrich Gauss and Adrien-Marie Legendre independently discovered the method of least squares, the essential feature of statistical regression. Least squares is a way to use data to make quantitative predictions. Those predictions are optimized so that, for any point in the data set, the model’s error multiplied by itself (squared) is minimized. Both Gauss and Legendre used the method of least squares to understand the orbits of comets, based on inexact measurements of the comets’ previous locations.

The dataset used for the first ever publicly demonstrated statistical regression by early 19th Century mathematician Adrien-Marie Legendre.
Legendre and Gauss’s problems were quite complex, but the method can be understood through a simple example. Imagine that you have a classroom of 5th graders. You are given the gender, height and weight of all the students. You are now told that one student is missing that day, but someone knows that student’s height and gender, but not his weight. So what’s the best guess for that student’s weight?
There are all sort of optimality criterion you could choose. You might like the criterion that minimizes the absolute error of your guess, or maybe one that has the least chance of being off by greater than 10 pounds. The least squares method optimizes by minimizing squared error.
So what makes squared error so special? Why did both Gauss and Legendre choose it, independently?
There are two main reasons that the squared error was almost immediately accepted by the mathematical community. First, at that time and to a lesser degree today, it was comparatively easy to compute. While there is a simple formula that can be used to get the best guess for minimizing the squared error, it’s a serious ordeal to calculate the best guess for almost any other optimality criterion — including absolute error.
Second, the estimate based on least squares has some nifty statistical properties. With some conditions, you can make the assumption that your error is normally distributed, which is pretty nice for understanding how confident you can be in your guess.
You gotta love a good normal distribution joke; Via Robert Buxbaum
Legendre was the first to make his discovery of the least squares method public. In his 1805 paper, “New Methods for Determination of the Orbits of Comets,” Legendre supplied the original articulation and example of the use of least squares regression. Legendre was confident that his method was a winner:
“Of all the principles which can be proposed for [making estimates from a sample], I think there is none more general, more exact, and more easy of application, than that of which we have made use… which consists of rendering the sum of the squares of the errors a minimum.”
Unfortunately for Legendre’s legacy, one of history’s most brilliant scientific minds was working on this same problem.
***

Carl Friedrich Gauss was one of history’s greatest mathematicians and maybe kind of a jerk.
Due to his astonishing contributions to mathematics, Carl Friedrich Gauss is sometimes called the “Prince of Mathematicians.” Although Legendre recognized Gauss’s genius, he probably had some less kind names he liked to call him. In a move of academic indecency, Gauss stole credit for Legendre’s discovery of least squares regression right out from under him.
In Gauss’s 1809 treatise, “Theory of the Motion of the Heavenly Bodies Moving About the Sun in Conic Sections,” the mathematician was able to solve the seemingly intractable problem of calculating planetary orbits. The central demonstration of his theory was Gauss’s ability to guess when and where the asteroid Ceres would appear in the night sky, an accomplishment no other scientist could claim. There was a great deal of complex math and geometry that went into his estimation, including the use of the method of least squares.
“Our principle, which we have made use of since 1795, has lately been published by Legendre….” Gauss wrote, “where several other properties of this principle have been explained.” Like most mathematicians at the time, Gauss liked to use the royal “we.”
Legendre was appalled. Gauss’s decision to claim a discovery that another mathematician had published before him was certainly questionable behavior. The noted statistics historian Stephen Stigler told us that, at the very least, Gauss’s decision was “insensitive.” Legendre sent a letter to Gauss to express his grave disappointment.
“It was with pleasure that I saw that in the course of your meditations you had hit on the same method which I had called the method of least squares in my memoir on comets… I confess to you that I do attach some value in this little find. I will therefore not conceal from you, Sir, that I felt some regret to see that in citing my memoir… you say [you had discovered it in 1795]. There is no discovery that one cannot claim for oneself by saying that one had found the same thing some years previously; but if one does not supply the evidence by citing the place where one has published it, this assertion becomes pointless and serves only to do a disservice to the true author of the discovery.”
Legendre ended the note with a statement of halting respect.
“You have treasure enough of your own, Sir, to have no need to envy anyone; and I am perfectly satisfied, besides, that I have reason to complain of the expression only and by no means of the intention.”
Gauss would never to back down from his contention that he had discovered the method first. Although not entirely conclusive, the preponderance of evidence suggests Gauss was telling the truth. Colleagues of Gauss agree that he had explained least squares to them and there are calculations in his notebooks that likely could not have been done by any other method.
Gauss had not published his finding because of his preference for fulling developing his ideas before making them public. Gauss famously lived by the motto, “Few, but ripe.” The mathematical historian Eric Temple Bell believes that if Gauss had published all of his theories when they came to him, mathematics would have been advanced by more than 50 years.
Today, Gauss receives most of the credit for the invention of least squares, and thus regression. This is primarily because Gauss’s explanation was so much more fully realized than Legendre’s. Stigler explains, “When Gauss did publish on least squares, he went far beyond Legendre in both conceptual and technical development, linking the method to probability and providing algorithms for the computation of estimates.”
Gauss did not think much of his use of least squares, dismissing it as “not the greatest of my discoveries.” He once wrote to a colleague of how embarrassed he was for his predecessors that they had not found it. He added that he wouldn’t publicize their oversight because of his distaste for “minxit in patrios cineres,” which translates to “urinating on the ashes of my ancestors.”
Still, Gauss remained troubled throughout his life that people had questioned his claim to regression. The statistical historian R.L. Plackett wrote of Gauss’s “less than wholehearted [acceptance] of the principle that publication establishes priority.”
Stigler told us that these kinds of priority disagreements are common in the history of scientific discovery. He explained, “The existence of a priority dispute is a sign that something important is going on.”
***

Although they were the creators of regression’s main feature, neither Gauss or Legendre used the word “regression” to refer to their method.
The term regression was first applied to statistics by the polymath Francis Galton. Galton is a major figure in the development of statistics and genetics. Unfortunately, his studies of inheritance led to him to invent the term eugenics and advocate for the breeding of a “better” society.
Galton used the term regression to explain a phenomenon he observed in nature. In the 1870s Galton collected data on the height of the descendants of extremely tall and extremely short trees. He wanted to know how “co-related” trees were to their parents. Galton published his analysis of his data in the 1886 paper Regression Towards Mediocrity in Hereditary Stature.
“It appeared from these experiments that the offspring did not tend to resemble their parents seeds in size, but to be always more mediocre than they – to be smaller than the parents, if the parents were large; to be larger than the parents, if the parents were small.”
We now refer to this phenomenon that Galton discovered as regression to the mean. If today is extremely hot, you should probably expect tomorrow to be hot, but not quite as hot as today. If a baseball player just had by far the best season of his career, his next year is likely to be a disappointment. Extreme events tend to be followed by something closer to the norm.
“Regression” came to be associated with the least squares method of prediction by the late 1800s. Karl Pearson, among the founders of mathematical statistics and a colleague of Galton’s, noticed that if you plotted the height of parents on the x-axis and their children on the y-axis, the line that best fit the data according to least squares had a slope of less than one. A slope of less than one is essentially the mathematical representation of “regression to the mean.” Pearson referred to this slope on a graph as the “regression line.” And thus the method of least squares and regression became somewhat synonymous.
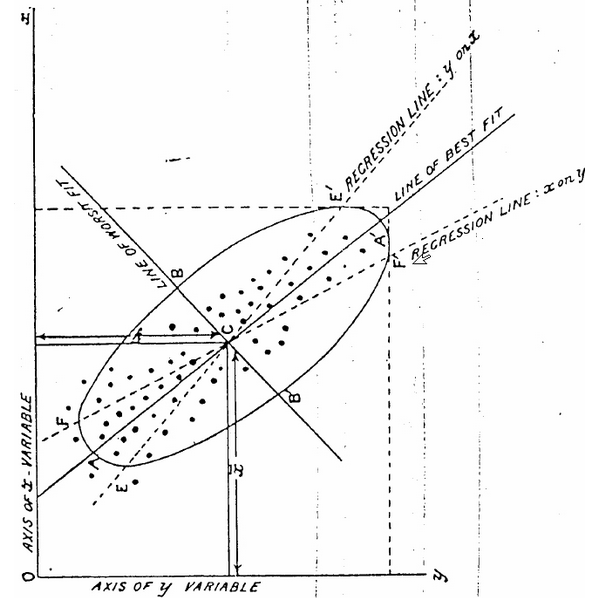
By 1901, the statistician Karl Pearson was using the “regression line” to refer to least squares estimate.
Regression analysis as we know it today is primarily the work of R.A. Fisher, one the most renowned statisticians of the 20th Century. Fisher combined the work of Gauss and Pearson to develop a fully realized theory of the properties of least squares estimation. Due to Fisher’s work, regression analysis is not just used for prediction and understanding correlations, but for inference about the relationship between a factor and an outcome (sometimes inappropriately). Post Fisher, there have been a variety of important extensions of regression including logistic regression, nonparametric regression, Bayesian regression, and regression that incorporates regularization.
Computing technology brought regression into the mainstream. In the 1920s, IBM created mechanical punched card tabulators that could be used to calculate the answers to computationally heavy statistical analyses like regressions. Before this, all calculations had to be done by hand, so regression was only for very small datasets or for those willing to do a mind numbing number of multiplication problems. Even still, all the way up to the 1970s, the computations to complete a regression could take days and the technology was only available to select researchers. It was not until the emergence of the modern desktop computer that the use of regression analysis was truly democratized. Today, anyone with access to a PC can run a regression for a moderately sized dataset in less than a second.
***
Gauss and Legendre would be amazed at the ubiquity of least squares regression today. Regression analyses are frequently used by academics, policy analysts, journalists and even sports teams to predict the future and understand the past. Even with the development of increasingly sophisticated algorithms for prediction and inference, good old least squares regression is still perhaps the crown jewel of statistical analysis.
Our next post is about a woman trying to get the neglected story of the Philippines in World War II written into textbooks.
To get notified when we post it → join our email list.
![]()
This post was written by Dan Kopf; follow him on Twitter here.