One of the greatest minds in 20th Century statistics was not a scholar. He brewed beer.
Guinness brewer William S. Gosset’s work is responsible for inspiring the concept of statistical significance, industrial quality control, efficient design of experiments and, not least of all, consistently great tasting beer.
But Gosset is certainly no household name. Books and articles about him are sparse, and he is rarely discussed among history’s most important statisticians. Because he used a pseudonym, his name isn’t even familiar to most people who frequently use his most famous discovery. Gosset is the “student” of the Student’s T-Test, a method for interpreting what can be extrapolated from a small sample of data.
How did a brewer of dry stout revolutionize statistics? And why is he so little-known?
Gosset made his great innovations while working as a brewer for Guinness from 1899 to 1937.
A Gentleman Scientist
By all historical accounts, William S. Gosset was a pretty awesome guy.
Contemporary statisticians like W. Edward Deming, Udny Yule, and Florence Nightingale David, respectively called him a “very humble and pleasing personality,” “very pleasant chap” and “A nice man […] without a jealous bone in his body.” Both Karl Pearson and R.A. Fisher, the two most famous statistical thinkers of the early 20th Century, who were known to hate each other, found common ground in their fondness for Gosset.
Born in 1876 in Canterbury, England, Gosset entered a world of enormous privilege. His father was a Colonel in the Royal Engineers, and though he intended to follow in his footsteps, he was unable to due to bad eyesight. Instead, Gosset attended the prestigious Winchester College, and then Oxford, where he studied mathematics and natural sciences. Soon after graduating from Oxford, in 1899, Gosset joined the Guinness brewery in Dublin, Ireland, as an experimental brewer.
In a delightful retrospective on Gosset’s achievements, the economist Stephen Ziliak writes colorfully of the young Gosset:
Gosset was in 1899 an energetic—if slightly loony—23 year-old gentleman scientist. He possessed a wickedly fertile imagination and more energy and focus than a St. Bernard in a snowstorm. An obsessive observer, counter, cyclist, and cricket nut, the self-styled brewer had a sizzle for invention, experiment, and the great outdoors.
Gosset would spend the rest of his life working for Guinness, and it was through working on Guinness products that he would develop his great statistical innovations.
The science that is part of the brewing process inspired Gosset’s statistical innovations.
When Gosset began working at Guinness, it was already the world’s largest brewery. Even compared to modern companies, Guinness was unusually focused on using science to improve its products. They hired the “brightest young men they could find” as scientists, and gave them liberal license to innovate and implement their findings. Perhaps the equivalent of being a computer scientist at Bell Labs in the 1970s or an artificial intelligence researcher at Google today, it was a wonderful job for the inquisitive and practical minded Gosset.
At that time, Guinness’s primary focus was maintaining the quality of its beer, while increasing quantity and decreasing costs. Between 1887 and 1914, the output of the brewery doubled, reaching almost one billion pints. How could the company increase production, while keeping its beer tasting as consumers expected? Gosset was assigned as part of the team that would answer that question.
Like most beers, Guinness is flavored with the flowers of the plant Humulus lupulus, also known as “hops”. The brewery used nearly five million pounds of the stuff in 1898. They determined which hops to use based on qualitative measures such as “looks and fragrance.”
At the scale at which Guinness was brewing, the “looks and fragrance” method was not economical or even accurate. The scientific brewing team, of which Gosset was a part, would improve this selection process.
Gosset’s first boss, the “scientific brewer” Thomas B. Case, believed that the best way to determine the quality of hops was by calculating the proportion of “soft” resins to “hard” resins in a batch (resins are a semisolid substance that comes out of the glands of the hops).
Case decided to take a small number of samples from different batches of hops from Kent, England, and calculate the percentage of soft resins to hard resins. He found an average of 8.1% of soft resins in one batch of eleven samples, and in another sample of fourteen, 8.4% of soft resins. What did these numbers mean for the consistency of hops across batches? Case didn’t really know. He looked at the data and couldn’t “support” any particular conclusion, but Case knew they would want to solve this problem in order to analyze such data in the future.
And so he turned to Gosset. The historian Joan Fisher Box explains that Gosset was called upon because he had studied a bit of Math at Oxford and was “less scared” of this kind of problem than the other brewers.
For a quantitative researcher working today, it is almost unfathomable to imagine, but at that time, a theory of making inferences from small samples did not exist. Of course, people periodically used small samples as evidence for conclusions, but they had no way of measuring the likely accuracy of their estimate. All methods for extrapolating from a sample relied on the idea that you had a large sample size, well over 30 observations, and could use the “standard normal distribution.” While this was true for most academic studies of the day, in many industrial settings, it was not possible to get such a large sample. Even a “scientifically minded” company like Guiness was limited in the amount of its product it could dedicate to testing.
Gosset discovered Student’s t-distribution; via Columbia University.
So Gosset set to work. His goal was to understand just how much less representative a sample is when the sample is small. In more technical terms, how much wider is the error distribution of an estimate when you only have a sample of two or ten, compared to when you have a sample of a thousand?
Gosset’s first problem involved figuring out exactly how many observations of malt extract, a substance used in beer making, were necessary to be confident the “degrees saccharine” of the extract was within 0.5 degrees of a targeted goal of 133 degrees.
His initial approach was just to simulate a whole bunch of data. He had an extract for which he had a very large number of samples and could be relatively confident of the exact degrees saccharine. He then took many different two-observation samples from the extract in order to test the accuracy of such a small sample. He found that about 80% of the time, the measurement from just two observations was within 0.5 degrees of the true number.
He then tried the same thing with three measurements. This time, there was an approximate 87.5% chance of getting with 0.5 degrees. With four measurements, he found a better than 92% chance. With 82 measurements, the likelihood of getting within 0.5 degrees was “practically infinite”.
His bosses at Guinness were thrilled with the findings. This would allow them to make intelligent decisions about which materials to use for their beer, in a way that no other business could.
Yet Gosset was not satisfied with his approximated method. He wanted to uncover the exact mathematics behind inference from small samples. He told Guinness that he wanted to consult with “some mathematical physicist” on the matter. The company obliged and sent Gosset to Karl Pearson’s lab at the University College London. Pearson was one of the leading scientific figures of his time and the man later credited with establishing the field of statistics.
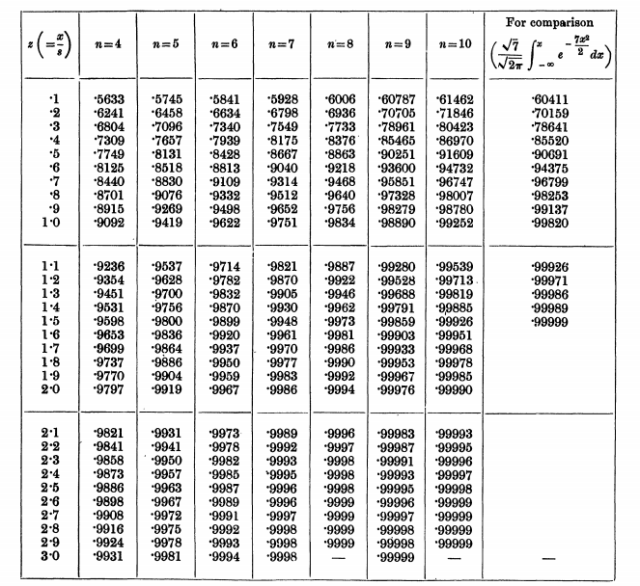
The original t-distribution table from Gosset’s seminal work, “The Probable Error of the Mean.”
How Gosset Became the “Student”
After a year spent on sabbatical at Pearson’s lab, Gosset had worked out the math behind a “law of errors” when working with small samples. Today, we know his discovery as the “Student’s t-distribution”. It is the primary way to understand the likely error of an estimate depending on your sample size and remains highly depended upon by those in academia and industry. It is among the pillars of modern statistics, and among the first things learned in introductory statistics courses. It is the source of the concept of “statistical significance.”
But why is it the “Student’s” t-distribution rather than “Gosset’s”?
Upon completing his work on the t-distribution, Gosset was eager to make his work public. It was an important finding, and one he wanted to share with the wider world. The managers of Guinness were not so keen on this. They realized they had an advantage over the competition by using this method, and were not excited about relinquishing that leg up. If Gosset were to publish the paper, other breweries would be on to them.
So they came to a compromise. Guinness agreed to allow Gosset to publish the finding, as long as he used a pseudonym. This way, competitors would not be able to realize that someone on Guinness’s payroll was doing such research, and figure out that the company’s scientifically enlightened approach was key to their success.
So Gosset published his article introducing the t-distribution, “The Probable Error of the Mean”, under the name “Student.” “The Probable Error of the Mean” is a relatively dry piece of work, mostly made up of mathematical derivations and a Monte Carlo simulation to demonstrate the accuracy of his method.
Though Gosset’s paper was, at the outset, mostly ignored by statistical researchers, a young mathematician named R.A. Fisher read the paper and was exhilarated by Gosset’s results and approach. Fisher was especially taken by the Gosset’s idea that his distribution table could be used to get a sense of how likely a certain result would be, compared to random chance, and that if the chances were low, we might consider the result “significant.” Fisher’s response to Gosset’s work would have major ramifications for modern science.

R.A. Fisher is the “Father of Modern Statistics” and, perhaps unfortunately, extended Gosset’s ideas in a more stringent direction.
Fisher’s Extensions and the Sanctification of .05
The British scientist and author Richard Dawkins called R.A. Fisher “a genius who almost single-handedly created the foundations for modern statistical science.” Some of Fisher’s most important work include his theories of experimental design, analysis of variance, and introducing the concept of making guesses of unknowns based on maximum likelihood (the concept of approximating an unknown value based on the number that makes related data most likely). On top of all this, he was a hugely influential biologist.
Fisher began studying mathematics at Cambridge University just one year after Gosset published “The Probable Error of Means.” Fisher knew Gosset was on to something big.
Gosset’s t-distribution and the idea of “statistical significance”, discussed using slightly different terms by Gosset, became fundamental to Fisher’s ideas about statistical methods. In 1925, Fisher published what would become arguably the most influential book in the history of statistics, Statistical Methods for Research Workers, which presented Gosset and Fisher’s work to a wider public.
Some of Fisher’s extensions of Gosset’s ideas were controversial. In fact, Gosset himself objected to some of them.
The most controversial of these was Fisher’s hallowing of a result that had a probability of less than 5% of occurring randomly (this probability is sometimes referred to as the p-value or P). For example, if a company surveyed people about which of two beers they preferred, they might find that 20 out of 25 surveyed preferred one beer. But how to decide whether this is enough evidence for the supremacy of that beer? Fisher suggests that if 20 people out of 25 choosing one beer is less than 5% likely to happen at random if people actually like the beers equally, then we can be comfortable using this as evidence. He wrote in Statistical Methods for Research Workers:
“The value for which P = .05, or 1 in 20… it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not. Deviations exceeding twice the standard deviation are thus formally regarded as significant.”
In the paper Guinnessometrics, the economist Stephen Ziliak demonstrates that Gosset found the .05 threshold to be arbitrary.
Gosset was more concerned with whether a result was practically meaningful than whether it was statistically “significant.” He referred to the concept of statistical significance itself as being “nearly valueless.” Gosset thought the evidence should be assessed depending on the “importance of the issues at stake” and not “some outside authority in mathematics.” Ziliak believes that Gosset approached his work with a Bayesian philosophy, a philosophy that generally opposes the still popular “Fisherian” approach of null hypothesis testing, rejecting or accepting a hypothesis based on a threshold p-value.
Today, many statisticians feel that that Fisher’s assertion that .05 signifies significance has done serious damage to science. The doctor and researcher John Ioannidis demonstrated that a large proportion of research findings published in scientific journals are false, in large part because of the reliance on the .05 threshold. Given the huge number of studies that are conducted every year, and the fact that one in twenty studies will meet the .05 threshold by random chance, many studies that purport to have detected a “significant” finding are spurious.
Gosset was a skeptical man who always considered context. Over the course of his life, he would never use the .05 rule that Fisher created out of his work. Gosset once referred to a p-value of .13 as being “a fairly good fit.” Gosset also thought a p-value of .02 was not necessarily evidence that a finding is accurate, “whether one would be content with that or would require further work would depend on the importance of the conclusion and the difficulty of obtaining [additional data].”
Gosset’s ideas are part of the basis for industrial quality control.
The Original Six Sigma Blackbelt
What little fame Gosset has today is primarily among students of statistics. But perhaps his widest impact is as a pioneer of industrial quality control.
The industrial revolution and modern factory methods led to product creation at a scale and speed never before seen. Prior to this scaled production, it was generally possible to check the quality of your goods using qualitative methods. Bread makers, boat builders and brewers made so little product that they could generally check each individually for quality issues. Industrial production brought with it great benefits, but also the challenge of how to make sure you didn’t ruin your brand’s reputation by letting faulty product slip through the cracks.
Gosset’s work was a boon to industrialists. He demonstrated to producers how many random samples they needed to check, in order to get a sense of the quality of the whole. His methods are now an almost standard part of factory protocol. Gosset’s work came many years before that of W. Edward Demings, considered by many the father of the quality evolution, and “six sigma”, a quality control methodology that relies heavily on Gosset’s ideas.
The mathematician John D. Cook finds it “unsurprising” that quality control would be founded by a brewer. He explains that unlike wine makers, who value variation, brewers “pride themselves on consistency.”
Gosset’s ideas about agricultural experimental design were also extremely influential.
***
Though the discovery of the t-distribution was Gosset’s grand achievement, he also had several other influential statistical ideas. Gosset developed a theory of efficient field experiment design and methods for applying statistical techniques to experimental data. Gosset would publish all but one article under the “student” pseudonym, only once releasing an article under his own name. The economist Heinz Kohler writes, “For many years, an air of romanticism surrounded the appearance of ‘Student’s’ papers, and only a few individuals knew his real identity, even for some time after his death.”
Yet given Gosset’s incredible impactful, he remains little known. He is rarely listed among history’s most important statisticians, though it can be argued that he deserves this recognition. His Wikipedia page is measly (580 words) in comparison to his peers (the pages of R.A. Fisher and Karl Pearson have over 3,000 words).
Certainly, part of the reason for this is that Gosset worked in business rather than academia. Had he been a professor like Fisher and Pearson, he would have been able to use his own name in his work, and perhaps publish textbooks detailing his methods and ideas. But if he worked outside of industry, he may never have had the opportunity to take on the practical problems that seem to have most stimulated him.
Perhaps just as important to Gosset’s absence of renown was his lack of ideology. Fisher, who would take his ideas and make them famous, was a man who believed in creating rules and structures for how quantitative research ought be done. Gosset was never stuck to any particular method. He was simply interested in solving the problems that would make sure each beer was as good as the last one.
![]()
For our next post, we examine how Auto-Tune changed the economics of the recording industry and ushered in a new era of music. To get notified when we post it → join our email list.
This post was written by Dan Kopf; follow him on Twitter here.