
This post is adapted from the blog of Udemy, a Priceonomics customer. Photo by thenails
The two men had decided that a second Great Depression was imminent.
The first man, John Gutfreund, was the CEO of Salomon Brothers. Business Week had dubbed him the “King of Wall Street” in 1985. The second man, Craig Coats Jr., led Salomon Brothers’ government-bond trading group. The year was 1987, and Michael Lewis, who would one day become a famous chronicler of Wall Street, was a young trader witnessing investors scramble to address the stock market crash now known as Black Monday.
Once Gutfreund and Coats Jr. decided that Black Monday was the Great Crash of 1929 come again, they bought $2 billion worth of 30-year U.S. Treasury bonds. American Treasury bonds are the safest investment out there, and incredibly popular during crashes and recessions. By buying the bonds, the two investors hoped to get out in front of investors’ flight to safety.
At the same time, a very different group of Salomon traders came to a very different conclusion. These men were a new breed on Wall Street. Unlike the brash, instinctive traders who populated Wall Street firms, they were quiet and esoteric former academics. While Gutfreund and Coats Jr. bet big on the panic turning into a depression, the “polite and mild-mannered and hesitant” academics bet big that everything would soon return to normal.
Time proved the academics right. Several years of strong economic growth followed Black Monday. Coats Jr.’s trade lost Salomon $75 million. The academics’ trade earned $50 million.
As Michael Lewis writes, it was a transition moment: the transfer of power on Wall Street from cursing, alpha-male traders to nerds with formulas.
Seven years later, the nerds started their own hedge fund, Long-Term Capital Management. The fund exemplified the rise of Wall Street quants. Two of its advisers, Professors Robert Merton of Harvard and Myron Scholes of Stanford, had invented a formula used by every options trader. Their financial models spawned the derivatives market and won them the Nobel Prize in economics.
Long-Term Capital raked in tremendous profits for 4 years. In its 5th year, the effects of the Asian and Russian financial crises nearly bankrupted the firm, and the New York Federal Reserve had to orchestrate a bailout.
Depending on whom you ask, Long-Term Capital Management was either the victim of unforeseen market forces—or an early warning that the foundation of the modern financial system is a disaster.
The Black-Scholes Formula
After the Financial Crisis of 2007-2008, “derivatives” became an ugly word.
A derivative is a financial instrument that derives its value from another asset, like a stock or a house. “They are investments in investments,” mathematician Ian Stewart wrote in 2012. “Promises about promises.”
In 2010, when people worried that no one knew the worth of Wall Street’s “toxic assets,” they were talking about derivatives like collateralized debt obligations: a promise to pay an investor a portion of the cash that flows in from sources like mortgage payments or stock dividends.

Photo by Martin Ceralde
Yet when Robert Merton and Myron Scholes won the Nobel Prize in 1997—for work that gained prominence in the 1970s—the Nobel committee praised them (and Fischer Black, their deceased colleague) for “develop[ing] a pioneering formula for the valuation of stock options.” In other words, for figuring out exactly how to price a derivative.
The research that earned Black and Scholes a Nobel influenced the development of all types of derivative markets. But their famous formula describes one type of derivative: stock options. Since the thinking behind the formula became as ubiquitous as air on Wall Street, it’s worth understanding Black-Scholes.
When an investor buys a stock option, she buys the right to buy or sell that stock at a certain price in the future. For one investor, that option could be a form of insurance. It’s less risky to own Twitter’s $29 stock if you have the option to sell it for $28 a year from now. With the option in hand, even if Twitter’s stock price crashes, the most she can lose is one dollar per share.
For another investor, an option could be a way to bet on changes in stock prices without actually buying any stock. If he is sure Twitter’s stock price will drop, then he should buy the option to sell Twitter stock at $28 a share. If the share price drops to $10, then his option will make a profit of $18 per share.
Since options offer this flexibility, they are valuable. How valuable? And how does this value change as an option approaches the date when it has to be exercised? That’s the question that the Black-Scholes formula answers.
The formula rests on the idea that there is no such thing as a free lunch. If Twitter’s stock price falls to $20, the value of the option to sell Twitter stock at $28 should increase. After all, it’s now likely that the owner of the option will be able to buy shares of Twitter for $20 and sell them for $28. In a market full of profit-hungry traders who can buy and re-sell options before their end date, the price of an option will always adjust to changes in the price of the underlying stock. Otherwise options traders could make free money.
Since there are no free lunches, the price of an option should always be the difference you expect to see between the share price set by the option and the actual share price when the option comes due. In other words, if your option allows you to sell Twitter shares for $28 a year from now—and you expect Twitter shares to sell at $29 a year from now—the option is worth $1.
Once you factor in the interest rate to account for the fact that money today is worth more than money tomorrow—a simple modification no different from accounting for inflation–you can set up a simple equation and solve for the price of the option.
There’s just one problem: No one knows how much Twitter’s stock will be worth a year from now, and lots of smart people disagree on whether its price will rise or fall.
This is where the thinking behind Black-Scholes becomes more important than the formula itself. Black, Scholes, and Merton didn’t try to answer the question, “How much will the stock price rise or fall?” Instead they made an important assumption: that a stock’s price rises and falls in the same predictably unpredictable manner as dust buffeted by atoms and molecules in the air.
Video via Khan Academy
This may sound strange, but it was (and continues to be) a popular idea.
In 1970s academia, economists and mathematicians studying financial markets increasingly looked to physics for inspiration. Scientists had long observed that particles in liquids and gases move or shake without any apparent cause, and they believed that this was a sign of the existence of molecules and atoms whose erratic movements caused the motion.
In the 1900s, theorists like Albert Einstein, Jean Perrin, and Marian Smoluchowski explained how this motion worked. They found that particles moved randomly, but by using statistics, they could model the most likely paths that something buffeted by these randomly moving particles would follow.
Inspired by a French mathematician who had independently used the same statistical approach to model stock market prices in 1900, mathematicians and economists embraced this naturalistic view of the stock market. One protege who studied under the pioneers of the Black-Scholes Formula has said that he and other students would go to the physics library looking for concepts they could “jam into finance.”
If movements in the stock market are random, they can be modeled and managed. This is what Black-Scholes does. The formula does not try to predict how stock prices will change. Instead it assumes the future path of stocks’ prices will—just like the dust mite buffeted by atoms and molecules—follow a normal distribution, which means that small movements are much more likely than extreme movements.
With this assumption, the only variable needed to understand the normal distribution (the probability that a stock’s price will change by such and such an amount) is the stock’s volatility. Is the stock more like Twitter, whose share price has fluctuated between $50 and $25 over the past year? Or like General Electric, whose shares have only fluctuated between $29 and $23 over the past year? By looking at the stock’s volatility in the past, the Black-Scholes formula can model how a stock price may change and spit out the right price for an option.
If a stock’s price has been very volatile, which suggests that the stock price will move up and down a lot in the future, an option on that stock is more expensive. For more volatile stocks like Twitter, traders have to pay more for the certainty of owning an option.
Wall Street historians give the Black-Scholes formula enormous credit for the changes that took place in financial markets after the formula’s publication in 1973. Within several years, the formula came standard on the calculators held by every options trader, and the formula’s inventors and other academics applied the same reasoning to other derivatives.
Since the formula gave derivatives an agreed on price, they were no longer bets. Options and other derivatives became “virtual commodities in their own right.” This made derivatives easy to trade; it meant that banks and hedge funds could list derivatives as assets alongside stocks, real estate, and bonds.
Aided by deregulation and the rise of computers, the first major options exchanges opened in the 1970s, followed by a wave of derivatives exchanges around the world in the 1980s and early 1990s. Today, the derivatives market is worth $710 trillion. Or perhaps $1.2 quadrillion. Or perhaps some other amount that is larger than the world’s GDP.
Geeks Bearing Formulas
It often takes a crisis for new ideas to take hold. As the Black-Scholes formula was published, Wall Street experienced just such a shock.
The 1974 stock market crash was one of the worst downturns in history, and a recession followed. Wall Street historian Peter L. Bernstein credits the crash with forcing Wall Street firms to turn to academia for new ideas. “Reluctantly, they began to show interest in converting the abstract ideas of the academics into methods to control risk,” he writes, “and to staunch the losses their clients were suffering.”
But even during a crisis, dissertations and economic journals did not fit Wall Street’s aggressive climate. “Wall Street had started to hire [academics], but only for research, where they’d be out of harm’s way,” financial journalist Roger Lowenstein wrote of the early 1980s. “The eggheads were stigmatized as ‘quants,’ unfit for the man’s game of trading.”

Photo by Ramy Majouji
The academics needed a champion, and for the geeky traders of Salomon Brothers, that champion was a senior bond trader named John Meriwether.
Meriwether could hold his own in the raucous atmosphere of Salomon Brothers. When Salomon’s CEO challenged him to a $1 million hand of liar’s poker, Meriwether got the CEO to back off by insisting that they play for $10 million. Yet Meriwether also hired assistant professors and finance and mathematics PhDs as bond traders. As Michael Lewis writes, one prominent professor complained that Meriwether stole “an entire generation of academic talent.”
The academics did not fit in culturally at Salomon, but they prospered. Their group became the firm’s most profitable, and the key was Meriwether’s full confidence in his recruits’ talents. Michael Lewis compared him to Quentin Tarantino and Harold Ross: Meriwether was like “a gifted editor or brilliant director” who “had a nose for unusual people and the ability to persuade them to run with their talents.” Exhibit A: On Black Monday, the academics’ positions lost $120 million. In the heat of the panic, Meriwether followed a common pattern of his: he told his traders to double down on their favorite trades.
Those trades earned Salomon $50 million even as the Treasury bond trade made that day by the CEO and Coats Jr. lost $75 million. The nerds and their theories—dismissed by Wall Street big shots as “academia nuts” and “a lot of baloney”—had proven their legitimacy in a big way.
In 1994, the quants got their own hedge fund.
Meriwether had to leave Salomon Brothers in 1991 following a scandal in which the Securities and Exchange Commission investigated one of his traders for submitting illegal bids on Treasury bonds. Meriwether decided to start a new hedge fund, Long-Term Capital Management, that would recreate his trading group from Salomon.
His ambitions were—in the words of financial journalist Roger Lowenstein—“staggeringly ambitious.” He wanted investors to commit their money (and be unable to withdraw it in the face of losses) for 3 years. He wanted to charge fees of 25% of profits (in addition to fees of 2% of the assets under management) rather than the normal 20%. He wanted some of the finest minds in finance to join his startup. And he wanted to raise $2.5 billion.
Meriwether got most of what he wanted. Most of his nerdy recruits from Salomon joined Long-Term Capital, along with David Mullins, Alan Greenspan’s number two at the Federal Reserve. Robert Merton and Myron Scholes, whose work on the Black-Scholes formula made them both rumored candidates for the Nobel Prize, joined as advisors. Meriwether only locked up $1.5 billion in capital, but he got it on the terms he demanded, and Long-Term Capital was still in many ways the “largest startup ever.”
Long-Term Capital Management’s strong start came thanks to the transformation that Michael Lewis had witnessed in 1987: the nerds’ day had come. One financier who invested described the combination of Merton and Scholes as “mystique taken to a very high extreme.” Another investor, remembering Myron Scholes’s command of financial mathematics, said of the fundraising tour, “They used Myron to blow you away.”
The fund’s academic firepower also paid dividends later, when Meriwether negotiated access to big banks’ capital on unprecedentedly friendly terms. Everyone had FOMO over this hot, new fund. “It was generally believed,” Roger Lowenstein wrote in his history of Long-Term Capital Management, “that Long-Term had the benefit of superior, virtually fail-safe technology.”
In 1994, its first year, Meriwether and his traders turned every dollar invested in Long-Term Capital Management into $1.28 ($1.20 after their fees), and they were featured on the cover of Business Week. Over the next two years, the firm earned returns of 59% and 57% before fees. In its fourth year, its trades returned 25%, and Scholes and Merton won the Nobel Prize.
The Secret of Long-Term Capital Management
At Long-Term Capital Management, a group of extremely smart traders advised by brilliant academics had a huge amount of money to place in a complicated, high-stakes game.
Yet the central tenet of Long-Term Capital Management’s trading strategy can be summed up simply: they looked for mispriced assets and bet that their prices—and the market—would become more rational over time.
A simple example of a quintessential Long-Term Capital Management trade is the investment the quants made on Black Monday, 1987, when they worked at Salomon Brothers. The trade involved two very similar U.S. Treasury bonds.
When someone buys a Treasury bond, they are funding the U.S. government. In exchange for that funding, the federal government repays it with interest. But you can’t get rich buying Treasury bonds—the interest rate is very low. Investors feel so confident that the U.S. government will always be around to pay its debts that they consider Treasury bonds an almost risk-free investment. If you have money in a Money Market fund, you almost definitely own Treasury bonds.
The traders did not, however, buy Treasury bonds and collect the interest. Instead they bought one type of Treasury bond, a 29 ½-year Treasury bond, and sold short equivalent amounts of a 30-year Treasury bond.
As Michael Lewis writes, this gave the traders a “Swiss-like neutrality in the market.” If the value of Treasury bonds rose or fell, it would not impact their position.
The bonds were almost identical, but more traders were buying and selling the newer 30-year bond. This liquidity made the 30-year bond a safer, more tradeable asset. Since Wall Street prefered the newer bond, traders paid a slight premium for it, and it had a lower interest rate.
The trade the former academics made—by buying one bond and selling short the other—was a bet that the two bonds’ interest rates would converge. They had bought the 29 ½-year bond at a slight discount compared to the 30-year bond, and if the interest rates converged, their 29 ½-year bonds would be worth slightly more than the newer bonds they shorted.
It was a good trade. They were basically betting that two assets would, over time, look identical. And a 30-year and 29.5-year Treasury bond are basically identical. So over time, the interest rates converged, and the traders made a lot of money.

Photo by Kevin Hutchinson
Few of Long-Term Capital’s trades were so simple. But the bulk of their trades consisted of finding a mispriced asset or assets and betting that the discrepancy would disappear. When one of Meriwether’s recruits explained a trade, he exclaimed, “But they are priced so egregiously!”
The problem with the trades favored by the former academics is that they are not especially profitable. Betting that small differences between similar assets will disappear is like betting only on football games with evenly matched opponents. The only way to make a fortune is to bet a fortune. During pitches to investors, Scholes compared Long-Term Capital’s strategy to “vacuuming up nickels that others couldn’t see.” It was not hyperbole. In 1996, Long-Term Capital made .67 cents per dollar.
To ensure those nickels added up, Long-Term Capital placed huge bets and borrowed so it could bet even more. The firm was leveraged 30:1, which is why the $1.5 billion hedge fund had assets of over $100 billion and exposures sometimes calculated as $1 trillion. “The best minds were destroyed,” a Fortune reporter wrote after the fall, “by the oldest and most famously addictive drug in finance, leverage.”
John Meriwether and his traders were not, however, risk-takers gambling with other people’s money. They invested their own money in Long-Term Capital Management and plowed their enormous bonuses right back into the fund. They were true believers.
This ensured that when they fell, they fell hard.
Long-Term Capital’s trading strategies were not unique. The Black-Scholes formula and other academic work were public knowledge. Goldman Sachs, JPMorgan, and all the major players poached Meriwether’s Salomon traders and raided academia for mathematics and physics PhDs. Roger Lowenstein writes that the ubiquity of Long-Term Capital’s strategies meant that the spreads its traders bet on had narrowed, and the fund struggled to find enough bets to spend its capital on.
What differentiated Long-Term Capital traders was their faith in the market becoming more rational. We can see this by looking at another textbook Long-Term Capital trade: betting on volatility.
Since the Black-Scholes formula uses a stock’s volatility to calculate the price of a stock option, Long-Term Capital’s traders liked to look at option prices. If option prices were high, that meant investors expected the stock to be very volatile. And if the expected volatility was higher than normal, Long-Term Capital would bet that options prices and the volatility implied by those prices would return to historic norms. One junior trader recalls one of the former academics looking at a discrepency between the prices of similar derivatives and saying, “There can’t be that much risk… There is going to be a secular trend toward a more efficient market.”
Video via Khan Academy
This is obviously risky. It’s like selling insurance against big changes in stock prices. Except that since Long-Term Capital bought and sold options rather than stocks, they were insuring against investors’ expectations of volatility as much as volatility itself.
John Meriwether and co. knew that betting on volatility was risky: that’s Wall Street. But they believed that they knew exactly how risky each trade was, which meant that their overall returns would be profitable and predictable.
In letters to investors, Meriwether explained the exact odds of the fund losing 5%, 10%, 15%, and 20% of its money. Losing 20% or more would happen every one year out of fifty, and losing enough to bankrupt the fund was considered so rare that it would never happen. Long-Term Capital’s spokesman told the press, “Risk is a function of volatility. These things are quantifiable.”
In the summer of 1997, several Asian countries struggled to maintain the value of their currencies and their humming economies. The press switched from praising the region’s growth to describing countries like Thailand and Indonesia as “paper tigers.” News reports showed images of half-built skyscrapers and shuttered factories.
This was bad news for Long-Term Capital. The firm had bet that volatility would be low and that the premiums for low-risk assets (like brand new Treasury bonds) would lessen. Instead the opposite happened: Investors worried about a global downturn fled to safety. In some months, the firm only broke even, and Long-Term Capital had its lowest returns yet on the year.
Yet Meriwether and co. did not panic. While other investors got out of their positions, Long-Term Capital doubled down. The traders believed the Asian Crisis was an opportunity, just like Black Monday in 1987. They expected the market would calm eventually; in the meantime, investors’ flight to safety was the exact type of inefficiency and stupidity they exploited.
The fund continued to hire and moved into a posh new office. At the same time, the Nobel Committee awarded Merton and Scholes the Nobel Prize in economics. At the ceremony, the two professors sipped champagne and extolled how the derivatives market would allow investors to limit risk in the ongoing, uncertain market conditions.
But the Asian Crisis kept getting worse, and the market kept getting more erratic and volatile. Unprecedented events kept occurring: It was an article of faith among investors that Russia, a nuclear superpower, would not default. But then the Russian government decided that it preferred to pay Russian workers rather than bondholders, and the International Monetary Fund decided not to come to the rescue. The markets panicked.
In five weeks, Long-Term Capital came undone. As investors bought safe assets, the fund’s trades looked worse and worse. In one day, the firm lost $553 million. Although the press barely knew Long-Term Capital existed, over the course of the year, it lost billions. At one meeting, every trader reported losing money. “Can’t we ever make money,” one of them asked sarcastically, “just for one day?”
The firm’s partners started fundraising, hoping to find enough capital to keep them solvent until the madness ended. But people hesitated as the Asian and Russian Crises expanded, and the more generous the terms Meriwether offered, the more people realized that Long-Term Capital was in trouble.
In his book, Roger Lowenstein quotes John Maynard Keynes: “Markets can remain irrational longer than you can remain solvent.”
On September 23, 1998, the head of the New York Federal Reserve invited the CEOs of 14 major banks and brokerage houses to a meeting. He knew that Long-Term Capital Management was on the brink of insolvency. He also knew that everyone in the room had either invested in Long-Term Capital, lent it money, or become intertwined with it through their trades. He feared that the fall of Long-Term Capital could paralyze the entire financial industry. He proposed the banks form a bailout.
It was a tough sell. But in September 1998, the banks agreed on a $3.5 billion bailout plan. Meriwether and his team agreed to work on salary for an oversight committee that had a 3-year mandate to sell-off Long-Term Capital’s holdings.
The Fed did not spend any public money—it only cajoled private banks into doing so. Yet the press and the public criticized the bailout, and a familiar phrase dominated the stories: Long-Term Capital Management was “too big to fail.”
What This Means
After its sudden fall, the Long-Term Capital traders described themselves as victims of an unprecedented event. When the partners gave a presentation to investors to rehabilitate their image, the Wall Street Journal summarized their message: “Last year’s carnage was a once-in-a-lifetime event that wasn’t their fault.” In a later interview, a senior trader said, “I do think it was something that never happened before.”
But that’s only credible if you have the attention span of a child.
When traders used the Black-Scholes formula, they treated volatility as a constant. Volatility was like the force of gravity: something to be measured—in this case from past stock market returns—and plugged into a formula. Every other model similarly looked to the past to predict the future.
”What we did is rely on experience,” one Long-Term Capital trader told the New York Times. “And all science is based on experience. And if you’re not willing to draw any conclusions from experience, you might as well sit on your hands and do nothing.”
That is understandable. Reasonable even. But it raises an important question. What period is a good baseline period for the markets?
To measure the volatility of Twitter stock, should you look at the past 6 months? The past year? Its entire history since its IPO?
If you are looking at U.S. Treasury bonds, should you include periods like the Great Depression and September 11? Or are those outliers?
As Roger Lowenstein notes in When Genius Failed, at one point, Long-Term Capital lost more than they believed was possible on a trade involving U.S. Treasuries. “True, it had happened in 1987 and again in 1992,” Lowenstein writes. “But Long-Term’s models didn’t go back that far. As far as Long-Term knew, it was a once-in-a-lifetime occurrence—a practical impossibility.”
One could argue that models are helpful tools, and Long-Term Capital Management simply misused them. But the problem was not just that the fund’s models did not go far back enough, or that the fund was a bit too leveraged. The thinking behind models like the Black-Scholes formula simply did not allow for the existence of regular crises like Black Monday and the Asian Financial Crisis.
Remember, the Black-Scholes model treats stock prices like a dust mite buffeted by randomly-moving molecules. Under this thinking, changes in a stock price follow a normal distribution: the most common movements are small, and there is only a small percentage chance of extreme increases or decreases.
But critics of Black-Scholes thinking point out that extreme changes are the norm in financial markets. Consider the boom and bust of the dot com bubble, or the Roaring Twenties followed by the 1929 crash and the Great Depression. Events that the Black-Scholes model considers impossible or once in a lifetime events happen every five to ten years.
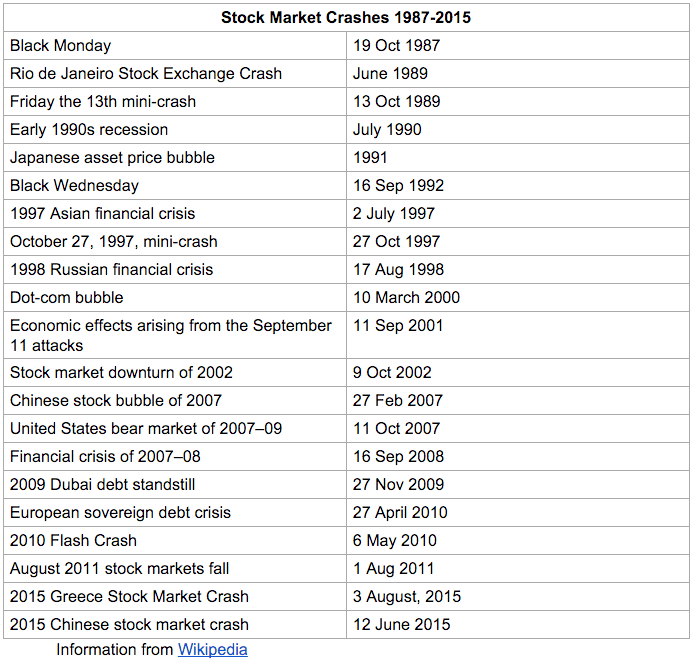
So other than sitting on their hands, what alternatives were available to Wall Street traders?
In 1999, Merton told the New York Times, “The solution is not to go back to the old, simple methods… the solution is greater complexity.” No amendment to the central problem of Black-Scholes normal distribution curve, however, has gained wide acceptance.
Legendary investor and contrarian Nassim Taleb accuses academia of exaggerating the importance of Black-Scholes to derivatives traders and encourages investors to trust their hard-earned instincts. He adds, however, that Black-Scholes misleads investors into believing they understand markets better than they actually do.
A major Long-Term Capital trader, Eric Rosenfeld, suggested after the firm’s failure that traders could use their models during “normal conditions” but needed “to buy insurance or have a pool of stand-by capital” for “when the world goes mad.” Insuring the world’s largest financial institutions, however, is not very practical, especially as they are supposed to be the insurers. And it’s not very profit-maximizing advice given the soft landing that bailouts provide.
Instead the status quo won out, and the lessons of Long-Term Capital Management were ignored. The New York Times predicted that investors would look askance at hedge funds after the firm’s failure, which is now laughable. Michael Lewis wrote that the partners’ careers might end in disgrace after being dragged in front of a Congressional Committee. Instead the traders all found lucrative new jobs at the banks that bailed them out. John Meriwether started a new hedge fund. It was profitable right up to the point that it folded during the 2008 financial crisis.
After 2008, “too big to fail” was back in the news on a grander scale, and so too were nerds and their formulas. Financial journalist Scott Patterson’s search for the origins of the crisis led him to write The Quants: How a New Breed of Math Whizzes Conquered Wall Street and Nearly Destroyed It. In 2009, Felix Salmon wrote an article for Wired about “the formula that killed Wall Street.”
The article was not about the Black-Scholes formula. It was about a gaussian copula function—created by David Li—whose purpose was to understand the correlations between different derivatives.
The similarities between it and Black-Scholes are stunning. Like Black-Scholes, Li’s formula enabled the creation of new derivative markets, which became worth north of $60 trillion. It also “made no allowance for unpredictability.” As Salmon writes, “It assumed that correlation was a constant rather than something mercurial.”
This was the same assumption Black-Scholes made about volatility, and traders measured correlations using Li’s formula by looking at time periods that did not reflect the ups and downs of the business cycle. When investors measured correlations in mortgage defaults, they looked only at a period when housing prices boomed.
The most striking similarity is that most of the industry expected David Li to follow in Scholes and Merton’s footsteps. “A year ago,” Salmon wrote in 2009, “it was hardly unthinkable that a math wizard like David X. Li might someday earn a Nobel Prize.” Instead the misuse of his formula led to the rise of gigantic derivatives markets that seemed reasonable but became toxic and full of unexpected defaults and losses in tough economic times.
On Wall Street, history repeats itself first as tragedy, then as farce, and then again and again in a series of bank bailouts.



