
![]()
By all accounts, Marilyn vos Savant was a child prodigy.
Born in St. Louis, Missouri in 1946, the young savant quickly developed an aptitude for math and science. At age 10, she was given two intelligence tests — the Stanford-Binet, and the Mega Test — both of which placed her mental capacity at that of a 23-year-old. She went on to be listed in the Guinness Book of World Records for having the “World’s Highest IQ,” and, as a result, gained international fame.
Despite her status as the “world’s smartest woman,” vos Savant maintained that attempts to measure intelligence were “useless,” and she rejected IQ tests as unreliable. In the mid-1980s, with free rein to choose a career path, she packed her bags and moved to New York City to be a writer.
Here, she caught a break: when Parade Magazine wrote a profile on her, readers responded with so many letters that the publication offered her a full-time job. Shortly thereafter, she established “Ask Marilyn,” a now-famous weekly column in which she answered (and continues to answer, to this day) a variety of academic questions and logic puzzles. It was in the body of one of these columns that vos Savant ignited one of the most heated statistical battles of the 21st century.
When vos Savant politely responded to a reader’s inquiry on the Monty Hall Problem, a then-relatively-unknown probability puzzle, she never could’ve imagined what would unfold: though her answer was correct, she received over 10,000 letters, many from noted scholars and Ph.Ds, informing her that she was a hare-brained idiot.
What ensued for vos Savant was a nightmarish journey, rife with name-calling, gender-based assumptions, and academic persecution.
The Monty Hall Problem: A Brief History

Imagine that you’re on a television game show and the host presents you with three closed doors. Behind one of them, sits a sparkling, brand-new Lincoln Continental; behind the other two, are smelly old goats. The host implores you to pick a door, and you select door #1. Then, the host, who is well-aware of what’s going on behind the scenes, opens door #3, revealing one of the goats.
“Now,” he says, turning toward you, “do you want to keep door #1, or do you want to switch to door #2?”
Statistically, which choice gets you the car: keeping your original door, or switching? If you, like most people, posit that your odds are 50-50, you’re wrong — unless, of course, you like goats as much as you like new cars, in which case you’ll win 100% of the time.
Loosely based on the famous television game show Let’s Make a Deal, the scenario presented above, better known as the “Monty Hall Problem,” is a rather famous probability question. Despite its deceptive simplicity, some of the world’s brightest minds — MIT professors, renowned mathematicians, and MacArthur “Genius” Fellows — have had trouble grasping its answer. For decades, it has sparked intense debates in classrooms and lecture halls.
Historically, the Monty Hall Problem was predated by several very similar puzzles.
In Joseph Bertrand’s box paradox (1889), three boxes are presented — one containing two gold coins, one containing two silver coins, and the final containing one of each. Assuming the participant draws one gold coin from a box, the problem then asks what the probability is that the other coin in that box is gold. Bertrand, who concluded that the probability was ⅔, was lauded for his ability to look beyond the obvious.
A second iteration of this paradox, the Three Prisoners Problem (1959), presents a statistically identical scenario, with the same outcome. “[It’s] a wonderfully confusing little problem,” its creator, Scientific American columnist Martin Gardner, later wrote, smugly. “In no other branch of mathematics is it so easy for experts to blunder as in probability theory.”
First presented in a letter to the editor of The American Statistician in 1975, the Monty Hall Problem was also counterintuitive. In this letter, Steve Selvin, a University of California, Berkeley professor, splayed out the situation in the intro of this article, and contended that switching doors yields a ⅔ chance of winning the car, whereas keeping the original door results in winning only ⅓ of the time.
Over the next decade or so, the Monty Hall Problem made several appearances, first in a Journal of Economics Perspectives puzzle by Barry Nalebuff, and subsequently in a 1989 issue of Bridge Today, by Phillip Martin. Neither man’s logic was refuted, and the problem generated relatively little attention.
Then, after 15 years without incident, the Monty Hall Problem was resurrected by Marilyn vos Savant — and an absolute shit-storm ensued.
Marilyn vos Savant’s Debacle

In September 1990, Marilyn vos Savant devoted one of her columns to a reader’s question, which presented a variation of the Monty Hall Problem:
“Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say #1, and the host, who knows what’s behind the doors, opens another door, say #3, which has a goat. He says to you, “Do you want to pick door #2?” Is it to your advantage to switch your choice of doors?”
“Yes; you should switch,” she replied. “The first door has a 1/3 chance of winning, but the second door has a 2/3 chance.”
Though her answer was correct, a vast swath of academics responded with outrage. In the proceeding months, vos Savant received more than 10,000 letters — including a pair from the Deputy Director of the Center for Defense Information, and a Research Mathematical Statistician from the National Institutes of Health — all of which contended that she was entirely incompetent:
You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I’ll explain. After the host reveals a goat, you now have a one-in-two chance of being correct. Whether you change your selection or not, the odds are the same. There is enough mathematical illiteracy in this country, and we don’t need the world’s highest IQ propagating more. Shame!
Scott Smith, Ph.D.
University of FloridaMay I suggest that you obtain and refer to a standard textbook on probability before you try to answer a question of this type again?
Charles Reid, Ph.D.
University of FloridaI am sure you will receive many letters on this topic from high school and college students. Perhaps you should keep a few addresses for help with future columns.
W. Robert Smith, Ph.D.
Georgia State UniversityYou are utterly incorrect about the game show question, and I hope this controversy will call some public attention to the serious national crisis in mathematical education. If you can admit your error, you will have contributed constructively towards the solution of a deplorable situation. How many irate mathematicians are needed to get you to change your mind?
E. Ray Bobo, Ph.D.
Georgetown UniversityYou made a mistake, but look at the positive side. If all those Ph.D.’s were wrong, the country would be in some very serious trouble.
Everett Harman, Ph.D.
U.S. Army Research InstituteYou are the goat!
Glenn Calkins
Western State CollegeMaybe women look at math problems differently than men.
Don Edwards
Sunriver, Oregon
The outcry was so tremendous that vos Savant was forced to devote three subsequent columns to explaining why her logic was correct. Even in the wake of her well-stated, clear responses, she continued to be berated. “I still think you’re wrong,” wrote one man, nearly a year later. “There is such a thing as female logic.”
Yet, the numbers behind vos Savant’s conclusion don’t lie.
Debunking the Monty Hall Problem
Since two doors (one containing a car, and the other a goat) remain after the host opens door #3, most would assume that the probability of selecting the car is ½. This is not the case.
“The winning odds of 1/3 on the first choice can’t go up to 1/2 just because the host opens a losing door,” writes vos Savant. Indeed, if you map out six games exploring all possible outcomes, it becomes clear that switching doors results in winning two-thirds (66.6%) of the time, and keeping your original door results in winning only one-third (33.3%) of the time:
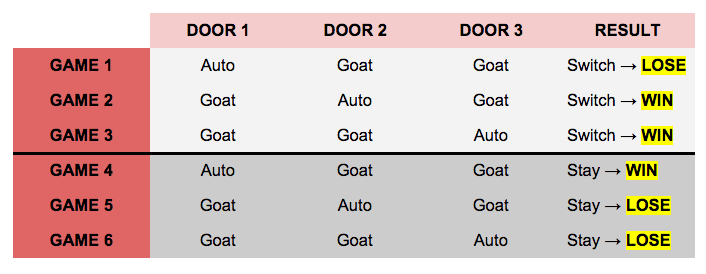
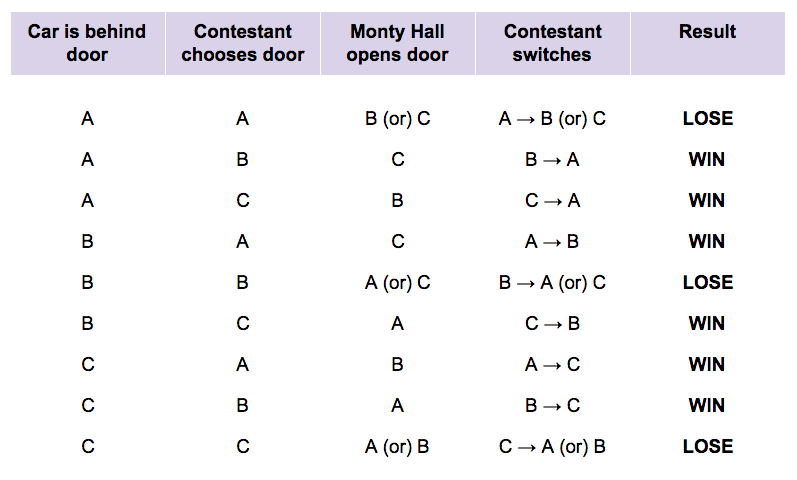
Another way to look at this is to break down every door-switching possibility. As we’ve delineated below, 6 out of the 9 possible scenarios (two-thirds) result in winning the car:
These results seem to go against our intuitive statistical impulses — so why does switching doors increase our odds of winning?
The short answer is that your initial odds of winning with door #1 (⅓) don’t change simply because the host reveals a goat behind door #3; instead, Hall’s action increases the odds to ⅔ that you’ll win by switching.
Here’s another way to visualize this. Imagine that instead of three doors, Monty Hall presents you with 100 doors; behind 99 of them are goats, and behind one of them is the car. You select door #1, and your initial odds of winning the car are now 1/100:

Then, let’s suppose that Monty Hall opens 98 of the other doors, revealing a goat behind each one. Now you’re left with two choices: keep door #1, or switch to door #100:

When you select door #1, there is a 99/100 chance that the car is behind one of the other doors. The fact that Monty Hall reveals 98 goats does not change these initial odds — it merely “shifts” that 99/100 chance to door #100. You can either stick with your original 1/100 odds pick, or switch to door #100, with a much higher probability of winning the car.
Still, while the math and numbers back up vos Savant’s assertion — that the odds of winning increase to ⅔ when you switch doors — one must consider other factors she doesn’t address in her answer.
The Psychology of Rationalization

Monty Hall, host of ‘Let’s Make a Deal’
In 1992, while the controversy over vos Savant’s answer brewed, Monty Hall — the game show host, and namesake of the problem — sat down for an interview with the New York Times.
Hall clarified that things worked a bit differently than the scenario presented by the Parade reader in vos Savant’s column. In the real show, for instance, he retained the authority to offer the contestant cash NOT to switch. Details like this, he said, altered the contestant’s mindset:
“[After I opened a door with a goat], they’d think the odds on their door had now gone up to 1 in 2, so they hated to give up the door no matter how much money I offered…The higher I got, the more [they] thought the car was behind [the other door]. I wanted to con [them] into switching there. That’s the kind of thing I can do when I’m in control of the game. You may think you have probability going for you when you follow the answer in her column, but there’s the psychological factor to consider.”
The “psychological factor” Hall mentions carries over from the show’s rules to the variation of the problem we’ve presented in this article. For contestants and problem-solvers alike, the Monty Hall Problem causes cognitive dissonance, a term psychologists use to describe the “mental stress experienced by an individual who holds two or more contradictory beliefs, ideas, or values at the same time, or is confronted by new information that conflicts with existing beliefs, ideas, or values.”
When people are confronted with evidence that is “inconsistent with their beliefs” (ie. the odds of winning by switching doors being ⅔, instead of ½), they first respond by refuting the information, then band together with like-minded dissenters and champion their own hard-set opinion. This is precisely the mentality of vos Savant’s thousands of naysayers.
***

More than 25 years later, arguments over the Monty Hall Problem’s semantics and vos Savant’s response still pervade — mainly centering around the intricacies of the host’s actions.
“Our brains are just not wired to do probability problems very well, so I’m not surprised there were mistakes,” Stanford stats professor Persi Diaconis told a reporter, years ago. “[But] the strict argument would be that the question cannot be answered without knowing the motivation of the host.”
Eventually though, many of those who’d written in to correct vos Savant’s math backpedaled and ceded that they were in error.
An exercise proposed by vos Savant to better understand the problem was soon integrated in thousands of classrooms across the nation. Computer models were built that corroborated her logic, and support for her intellect was gradually restored. Whereas only 8% of readers had previously believed her logic to be true, this number had risen to 56% by the end of 1992, writes vos Savant; among academics, 35% initial support rose to 71%.
Among the new believers was Robert Sachs, a math professor at George Mason University, who’d originally written a nasty letter to vos Savant, telling her that she “blew it,” and offering to help “explain.” After realizing that he was, in fact, incorrect, he felt compelled to send her another letter — this time, repenting his self-righteousness.
“After removing my foot from my mouth I’m now eating humble pie,” he wrote. “I vowed as penance to answer all the people who wrote to castigate me. It’s been an intense professional embarrassment.”
Priceonomics has written two books. One is for skeptics, the other optimists. Choose your adventure → Everything is Bullshit or Hipster Business Models.
![]()
To get occasional notifications when we write blog posts, please sign up for our email list. This post was originally published on February 19, 2015.



